Measuring rainfall – it’s easy and difficult at the same time

Dr. Peggy LeMone is an NCAR Senior Scientist who studies weather and cloud formation.
UCAR
By Dr. Peggy LeMone
In early September of 2013, the Boulder, Colorado, area had huge amounts of rain. Which brings us to the questions - How do you measure rain? And how accurate are the measurements? Even though I have done weather research for many years, during this storm I was reminded how hard it is to measure rain accurately.
This is the story of my attempts to measure rain during the storm. It’s also about the many possible sources of error when making rain measurements – from old rain gauges to growing trees and even, possibly, inquisitive raccoons.
By Monday morning (September 16), I had measured over 16 inches in our backyard rain gauge from the storm which began September 10. The gauge is the same type the National Weather Service uses. It has a funnel that deposits rain into an inner tube with a smaller diameter (like this one), but bigger. The inner tube’s diameter is just small enough to make the depth of rain ten times what it would be in a gauge without the tube and funnel. Thus, each inch in the tube is equivalent to 0.1 inches (a tenth of an inch) of rainfall. This makes it easier to read accurately!
My gauge is old. I inherited it from a weather-observing neighbor who moved away. The funnel and inner tube doesn’t quite fit, so, I leave the gauge open and then pour the rain into the inner tube using the funnel.

The rain gauge
Peggy LeMone
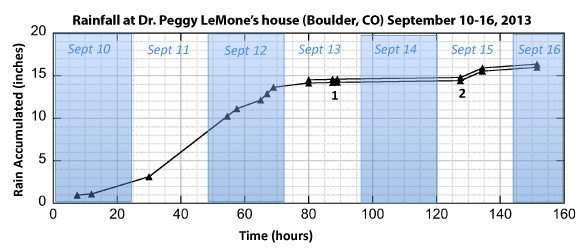
On the morning of September 12th, the gauge was so full and heavy, with over seven inches of rain, that I decided to stick a yardstick in the gauge to measure the rain amount, and save pouring into the inner tube for the end of the storm. The gauge tilts slightly, so I took a measurement on the uptilt side and the downtilt side and took an average. That evening I found that the bottom of the gauge sagged in the middle, leading to an even deeper measurement than the downtilt side. With these flaws, the lack of the ten-to-one exaggeration of depth, and some measurements being taken in the dark with a flashlight, my data were only approximate. I recorded measurements to within the nearest quarter inch (see the graph below).
Were my measurements accurate? On Friday morning, September 13, I took measurement using a more accurate method to compare with my estimates. After bailing out five full tubes of rain, I poured the remaining water through the funnel into the tube to a depth of 13.5 inches, spilling a little bit during this process. The result was 0.38 inches more than my rough estimate from the night before - a storm total of 14.52 inches up to this time. On the graph, this is marked as 1. (The lower shows the uncorrected values.)
But the rain hadn’t stopped. I awoke on the morning of September 15th and heard reports that up to 2 inches of rain fell overnight. I went outside to check our gauge – only to see that it had been knocked over (probably by raccoons). Fortunately, I have a second rain gauge in my backyard – a plastic gauge that registered about 0.25 inches. I added a conservative 0.2 inches, since this gauge was under trees (marked as 2 on the graph).
The final number: 16.37 inches on rain, more or less.
Why do I add “more or less”? Because there is uncertainty in the measurements. The metal gauge had been in the same place for several years, but I have moved it in the past year away from a growing tree. I noticed on September 13 that the tree had intruded again: the end of one branch was about 10-15 feet over the gauge, or slightly to the east. Runoff from this branch could have added to the total before I moved the gauge four feet to the west for the last two measurements. It is also possible that the 0.98 inches could be high, but I doubt it: I had briefly run a sprinkler hose at a low setting, but I had moved the gauge out of the way and I turned the water off immediately once the rain started. Switching the rain gauges adds uncertainty and so does the previously-mentioned spillage when I poured the remaining water in the gauge into the tube. Also, because my rain gauge was open at the top, some of the water could have evaporated, although evaporation was probably minimal, given the high relative humidity.

Looking up from where the rain gauge was before Time 2. The tree is to the north and east.
Peggy LeMone
The exposure of the rain gauge is undoubtedly the greatest source of error. According to the National Weather Service and CoCoRAHS (both of which use citizen volunteers to measure rainfall), “exposure” of the rain gauge is important. Rain may be blocked by nearby obstacles causing the number to be lower than it should. Or, rain may be blown into or away from the gauge by wind gusts. The recommendation is that the gauge be about twice the distance from the height of the nearest obstacles, but still sheltered from the wind.
The gauge was certainly sheltered from the wind. It is located about 10 feet south of the house, which is about 15 feet high, and to the west of a fence and small trees as well as the tree in the photograph. There is a much smaller tree to the southwest.
All the obstacles suggest that some rain could have been blocked from reaching the gauge, which would imply that the rainfall total is too small. On the other hand, some rain might have been running down the branch in the picture. (In fact, because of the large amount, I thought this might be the main effect before doing some research on exposure)
It is also recommended that the gauge be level, which it wasn’t. I’m not too worried about this, since it was nearly vertical.
The conclusion? There was a lot of rain. It could have been an inch more than my measurement or an inch less. Acknowledging this is called reporting error. It doesn’t mean that the measurements are wrong, it just gives an idea of how accurate they are. My total was not the largest; there were at least two other measurements near 18 inches.
Now that I’ve described all that can go wrong measuring rainfall, let me add that, putting a rain gauge in the right place, and taking an accurate rainfall measurement is fairly easy. If you have a perfect cylinder, simply stick a ruler in and read the depth (make sure to correct for any offset of the “zero” line and correct for this offset; and see if the ruler pushes the water level up very much).
If you have a bucket (or glass) with sides that aren’t straight up and down, you’ll need to do a bit of math to figure it out. Here’s what you’ll need to do:
- Measure the diameter of the bucket at the level of the rain. Subtract out twice the thickness of the walls.
- Measure the diameter of the bucket at the bottom in the same way.
- Calculate the average of the two diameters.
- Divide by two to find the average radius.
- Find the average volume of rain = Depth x radius x radius x 3.14.
- Find the area at the top of the bucket (this is the area over which the rain is collected).
- Measure the diameter
- Divide the diameter by 2 to get the radius
- Area = radius x radius x 3.14
- Divide the rainfall volume by this area to get the rainfall.
It would be an interesting exercise to put several buckets (or rain gauges) in different places in a field, your back yard, or your schoolyard to see how much the measurements vary. Soup cans, though not perfect, would work pretty well. I might try this during the next rainstorm. (I hope not too soon!)