How high is my drone flying?

Goal

Design and perform one or more experiments to help you identify a way to estimate your drone's height. Use your experience to judge which method provides the most accurate estimates.

If your drone doesn’t have a GPS unit, how can you figure out how high you’re flying?

Illustration of how to calculate how far off the ground a drone is flying

Materials

  • One or more UAV (Unmanned Aerial Vehicle or "drone") and the controller used to fly it
  • Football or soccer field with marked distances, or a measuring tape
  • Instrument for measuring elevation angles; either:
    • Angle-measuring app on a smartphone
    • Protractor inclinometer (find instructions online to make your own)
  • Scientific calculator (with trigonometric functions)

Directions

Encourage students to come up with their own ideas about how to measure height before they start. For example, they might suggest flying near something with a known height, such as a flagpole or a building.

Have students create a data table (like the one below) to record their measurements and results of calculations.

  Distance from Pilot to Observer (D) Observed angle to drone (a) Observed angle to the location directly below the drone (b) Drone height (H)
Example 30 feet 43° 10° 33.3 feet
Trial 1        
Trial 2        
Trial 3        

Think it through: Questions to consider

Before collecting data, have students discuss:

  • How many trials will it take for you to feel confident your final answer is accurate?
  • How might you check if your answer is reasonable?

Fly and Collect Data

Set up a flight zone so the drone pilot and observer are a known distance apart. For instance, you might place the students on a sports field so they are 10 yards (30 feet) apart.

A man using a smart phone app for measuring altitude angle

Pilot: Have the student pilot fly the drone straight up and hover directly overhead at the height you want students to measure.

Observer: Have the student observer use a level app on a smartphone (or make and use a simple inclinometer) to:

  1. Measure and record the angle to the drone - students will use this value to calculate the height of the drone above eye level.
  2. Measure and record the angle to the spot directly below the drone - students will use this value to calculate the height of their eyes above the ground.
  3. Have students use the angles and formulas (which use the tangent function - tan - on a scientific calculator) to calculate the height of the drone above the ground.

Calculate Height

Students will use the two angle measurements together to calculate the height of the drone. As shown in the diagram below, the height (H) of the drone equals the height above eye level (A) of the drone plus the distance below eye level (B) of the location directly beneath the drone.

Height of drone equals distance up plus distance down from eye level

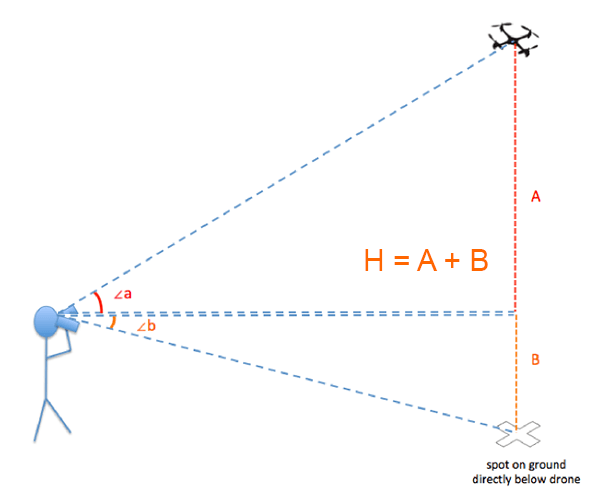
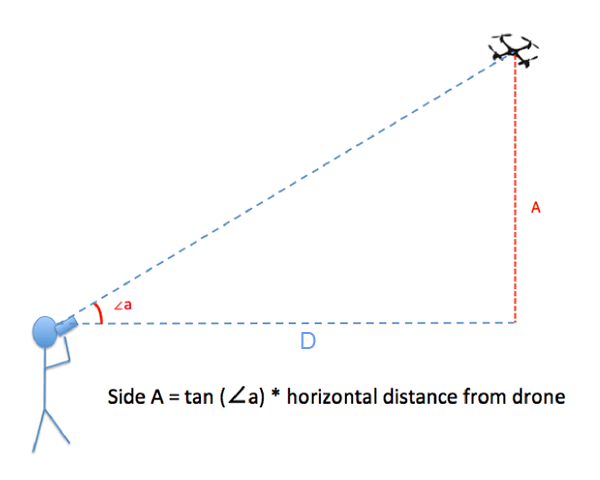
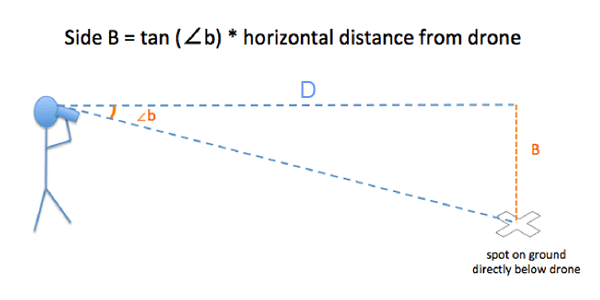
Students will use the horizontal distance to the drone (D) along with the tangent function ("tan" on a scientific calculator) to calculate the distance A from angle ∠a. They will use the horizontal distance (D), tangent function, and angle ∠b to calculate distance B.

Here is a sample calculation using the values in the Example row in the table above of D = 30 feet, ∠a = 43° and ∠b = 10°:

A = D x tan ∠a = (30 feet) x tan 43° = (30 feet) x 0.93 = 28 feet

B = D x tan ∠b = (30 feet) x tan 10° = (30 feet) x 0.18 = 5.3 feet

H = A + B = 28 feet + 5.3 feet = 33.3 feet

Measure angle up to drone to calculate height

Measure angle down to spot beneath drone to calculate height

Follow up

Ask students to discuss:

  • What can you do with the information about the height of your drone? For example, if students want to capture a time series of photos from a UAV, showing how a natural area looks every week over a year, how can they ensure that they are always flying at the same height?
  • How else might you use the technique you used to estimate height?
  • What other objects might you use this technique to measure?

Assessment

Have students present their results to classmates. Presentations should include data and results of calculations as well as responses to the questions in the Think it through: Questions to consider and Follow up sections above.

Credits

This activity was developed by LuAnn Dahlman for Earth Science Information Partners (ESIP).

Creative Commons Attribution-NonCommercial-ShareAlike license

It is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license.